1
Factor
Común
Se aplica en binomios, trinomios y
polinomios de cuatro términos o más.
No aplica para monomios.
- Es el primer caso que se debe
inspeccionar cuando se trata de
factorizar un polinomio.
- El factor común es aquello que se
encuentra multiplicando en cada uno de
los términos. Puede ser un número, una
letra, varias letras, un signo negativo,
una expresión algebraica (encerrada en
paréntesis) o combinaciones de todo lo
anterior.
-
De los coeficientes de los términos,
se extrae el MCD (Máximo Común
Divisor) de ellos.
- De las letras o expresiones en
paréntesis repetidas, se extrae la de
menor exponente.
- Se escribe el factor común, seguido
de un paréntesis donde se anota el
polinomio que queda después de que
el factor común ha abandonado cada
término.
ab + ac + ad = a ( b + c + d)
Ejemplo 1
(Hay factor común entre los números)
8a - 4b + 16c + 12d = 4. (2a - b + 4c + 3d)
Ejemplo 2:
(Hay factor común entre las letras)
7x2 + 11x3 - 4x5 + 3x4 - x8 = x2. (7 + 11x - 4x3 + 3x2 - x6)
2 Factor
Común por
Agrupación
de Términos
- Se aplica en polinomios que tienen 4,
6, 8 o más términos (siempre que el
número sea par) y donde ya se ha
verificado que no hay factor común
(caso 1).
-
Se forman grupos de igual número
de términos, buscando que exista
alguna familiaridad entre los términos
agrupados (es decir, que tengan
rasgos comunes). La agrupación se hace colocando
paréntesis.
- ¡CUIDADO! Deben cambiarse los
signos de los términos encerrados en
el paréntesis si éste queda precedido
por signo negativo.
- Se extrae factor común de cada
grupo formado (es decir, aplicamos el
caso 1 en cada expresión encerrada
en paréntesis).
- Por último, se extrae factor común
de toda la expresión (es decir,
nuevamente se aplica el caso 1; en
esta ocasión, el factor común es una
expresión encerrada en paréntesis)
ab+ac+bd+dc = (ab+ac)+(bd+dc)
Ejemplo 1
a2 + ab + ax + bx
(a2 + ab) + (ax + b)
a(a + b) + x(a +b)
(a + b) (a +x)
Ejemplo 2:
4am3 – 12 amn – m2 + 3n
= (4am3 – 12amn) – (m2 + 3n)
=4am (m2 – 3n) – (m2 + 3n)
R: (m2 – 3n)(4am-1)
3 Diferencia
de
Cuadrados
Perfectos
Expresiones como a2 - b2 , 42 - p2q2 , 1/9y2 - m2n2 , se denominan diferencias de cuadrados perfectos, ya que los términos que lo forman tienen raíz cuadrada exacta.
La diferencia de cuadrados perfectos se factoriza como el producto de dos binomios, uno como suma y otro como resta.Los términos de estos binomios son las raíces cuadradas de cada uno de los términos de la diferencia planteada al principio.
a2 − b2 = (a + b) · (a − b)
Ejemplo 1:
X2 - y 2x y = Raíces
Se multiplica la suma por la diferencia
R: = (x + y) (x- y)
Ejemplo 2:
100m2n4 - 169y6
10mn2 13y3 = Raíces
Se multiplica la suma por la diferencia
R: = (10mn2 + 13y3) (10mn2- 13y3)
4
Trinomio
Cuadrado
Perfecto
(TCP)
- El trinomio debe estar organizado en
forma ascendente o descendente
(cualquiera de las dos).
- Tanto el primero como el tercer
término deben ser positivos. Asimismo,
esos dos términos deben ser cuadrados
perfectos (es decir, deben tener raíz
cuadrada exacta). En otras palabras, el
primero y el tercer término deben
reunir las características de los términos
que conforman una Diferencia de
Cuadrados Perfectos
- Primero debemos verificar que se
trata de un Trinomio Cuadrado
Perfecto (TCP). Para ello extraemos la
raíz cuadrada tanto del primer como
del tercer término.
- Realizamos el doble producto de las
raíces obtenidas y comparamos con el
segundo término (sin fijarnos en el
signo de éste). Si efectivamente nos
da, entonces tenemos un TCP.
- La factorización de un TCP es un
binomio al cuadrado, que se
construye anotando las raíces
cuadradas del primer y tercer
término, y entre ellas el signo del
segundo término.
Ejemplo 1;
a2 – 2ab + b2
Raíz cuadrada de a2 = a
Raíz cuadrada de b2 = b
Doble producto sus raíces
(2 X a X b) 2ab (cumple)
R: (a – b) 2
Ejemplo 2:
49m 6– 70 am3n2 + 25 a2n4
Raíz cuadrada de 49m6 = 7m3
Raíz cuadrada de 25a2n4 = 5an2
Doble producto sus raíces
(2 X 7m3 X 5a2n2) = 70am3 n2 (cumple)
R: (7m – 5an2)
5
Trinomio
de la
forma x^2+bx+c
- Tienen un termino positivo elevado al cuadrado y con coeficiente 1 (
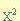) - Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).
- Tienen un termino independiente de la letra que aparece en los otros dos (+ o -).
Factorizar un trinomio de esta forma:
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
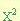. - El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Si los dos factores tienen signos iguales entonces se buscan dos números cuya suma sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.
- Si los dos factores tienen signos diferentes entonces se buscan dos números cuya diferencia sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”,
- el mayor de estos números será el segundo término del primer factor binomio, y el menor de estos números será el segundo término del segundo factor binomio.
Ejemplo 1
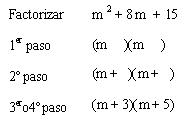
ejemplo 2
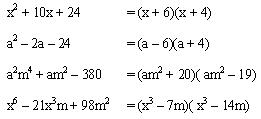
6 Trinomio
de la
forma ax^2+bx+c
Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado (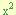
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
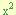) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:- Multiplicamos el coeficiente “a” de el factor “a
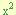” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a
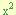” de la manera 
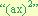. - Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
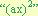la que seria “ax”. - al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.
Ejemplos
7 Cubo De Binomios Perfecto
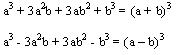
Para reconocerlo se deben tomar en cuenta los siguientes puntos:
Debe tener cuatro términos, y estar ordenado con respecto a una letra.
) y el 4º (b
), deben poseer raíz cúbica exacta.
].
, si hay términos negativos el resultado es el cubo de la diferencia de dos cantidades (a – b)
.
Ejemplo 1
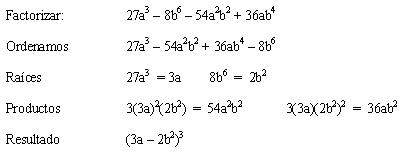
Ejemplos 2
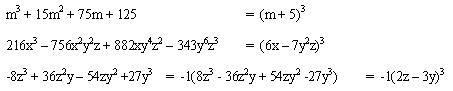
8 Suma y
Diferencia
de Cubos
Perfectos
- La suma de dos cubos perfectos se descompone en dos factores, el primero es la suma de sus raíces cúbicas, y el segundo se compone de el cuadrado de la primera raíz menos el producto de ambas raíces más el cuadrado de la segunda raíz.
- La diferencia de dos cubos perfectos se descompone en dos factores, el primero es la diferencia de sus raíces cúbicas, y el segundo se compone del cuadrado de la primera raíz más el producto de ambas raíces mas el cuadrado de la segunda raíz.
Ejemplo 1
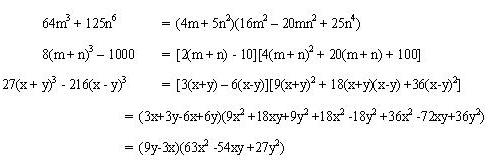
No hay comentarios:
Publicar un comentario